
| Home | Run Solver | User Guide | Programming |
|---|
The standard Sudoku board is a 9 by 9 array of cells. The challenge is to assign one of the values 1-9 to each cell such that each value occurs in exactly one cell of each row, each column, and each 3x3 box. Each puzzle starts with some of the cells filled with values (the clues), such that the puzzle has only one solution - there is exactly one way to fill in the open cells consistent with the rules. Puzzles are considered most satisfactory when they can be solved entirely by logic, without requiring trial and error. A sample Sudoku:

Rows are labelled with letters top-to-bottom and columns numbered left-to-right. The boxes are numbered across rows first, then columns - the upper left box is Box 1, the upper middle Box 2, the middle left Box 4, and so forth. The term "group" will refer to any set of cells required to contain 1 of each value, that is, a row, column, or box. Cells are referenced by row and column, for example, A4 is the fouth cell in the first row. A "choice" is any assignment of a value to a cell, such as 4 at A7, abbreviated 4@A7. A "possibility" will be any value for a given cell that has not been excluded.
The simplest strategy is to look for a value that is forced to occur in one particular cell of a box. This Single Position situation arises when all open cells of a box but one belong to rows or columns that already contain that value. Here, value 2 (green) can only go in one cell of Box 1 - all its other open cells are members of rows or columns that already contain a 2 (red).
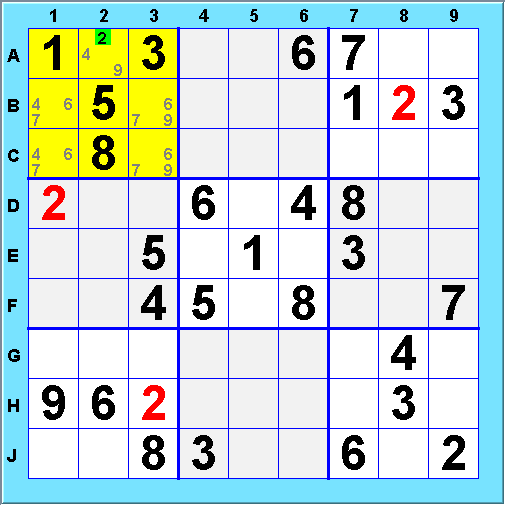
This kind of situation is fairly easy to find by looking at the rows and columns that intersect each box. There are many such singles in the example above; for example, in Box 6, 2 must go in F7 and 4 has to go in E9. The same logic applies to rows and columns (though boxes are a bit easier to scan). For example, in the same puzzle, value 8 is forced to go in cell A8 of Column 8. Note that this 8 was not a Single Position situation with respect to Row 1 or Box 3:
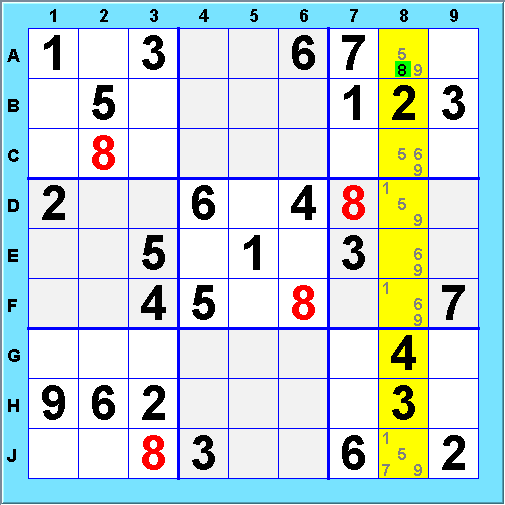
A second kind of single choice occurs when a cell is reduced to a Single Possibility. Finding these requires checking, for each cell, what values are already set in all of its groups. In the example below, Cell H7 is reduced to the single possibility 5 due to the competing values shown in red. Note that we don't highlight competing values outside the cell's box if they are already accounted for inside the box.

Enabling Notes makes Single Possibilities very easy to find.
Checking for the two kinds of singles is generally sufficient to solve Easy sudoku. More complex Sudokus require that we look at the sets of possibilities remaining in the open cells. The possibilities can be tracked by hand, or by enabling the Notes option in the Solver - the small gray numbers in the example displays.
The simplest strategy in this class is the Naked Pair. A Naked Pair occurs when a group contains two open cells with exactly the same pair of possible values. The pair is "naked" in the sense that there are no other possibilities in the cells. This configuration allows us to eliminate the pair's possibilities from all the other open cells in its group. Why? If either value is assigned to a cell outside the pair, there will be only one possibility left in the pair cells, so that one or the other will be left without a valid value. In the example below, there is a naked pair 2,8 (orange) in cells F7 and F9 (yellow) of Row F (green). This rules out 3 possibilities (red): 8 at F1, 2 at F4, and 2 at F5.

This reasoning applies to larger sets as well: Naked Triples, Naked Quads, and so forth. A Naked Set of size n occurs when a group contains a set of n open cells which have exactly n distinct possibilities among them. Even though we don't know which value will go in which cell of the set, we can remove its possibilities from the remaining open cells in the group. If one of the n values is assigned outside the Naked Set, then there will only be n-1 distinct possibilities to assign to the n Naked Set cells, making the puzzle unsolvable.
In looking for the larger naked sets, note that it is not necessary that each cell in the set contain all n values - all that is required is that the number of possibilities in the set as a whole is the same as the number of cells. For example, it is common to find a Naked Triple on values a,b,c appearing as 3 cells containing ab, bc, and abc. The fact that the possibility set can be different in each cell makes larger Naked Sets trickier to spot. In the next example, values 4, 5 and 7 in cells D2, D3 and E1 of Box 4 constitute a naked triple, eliminating 4@D1, 5@D1, 4@F1, and 7@F2. D2, D3, and E1 each have a different set of possibilities, but they form a naked triple because the union of their possibilities has just 3 values 4,5, and 7.

In a Naked Set, a set of values is bound to a specific set of cells because those cells have no other possibilities. A complementary way that a set of values and cells can be bound together is if the values have no other places to go. Suppose some group has several open cells but there are two values a and b that are possible in only two of the cells. That forces those two cells and values to go together, eliminating any other possibilities for the two cells. In this example, there's a hidden pair in Column 3 (green). Values 4 and 5 (orange) are only possible in cells B3 and E3. Since placing them will fill both cells, all other possibilities - 2 at B3, 9 at B3, 1 at E3, and 7 at E3 - are eliminated (red).

This type of situation is called a Hidden Set. The set is "hidden" because the cells of the set contain additional possibilities that make the key possibilities harder to spot. This method extends to larger sets of values and cells in the same way as Naked Sets. Look for a hidden triple in the following puzzle:
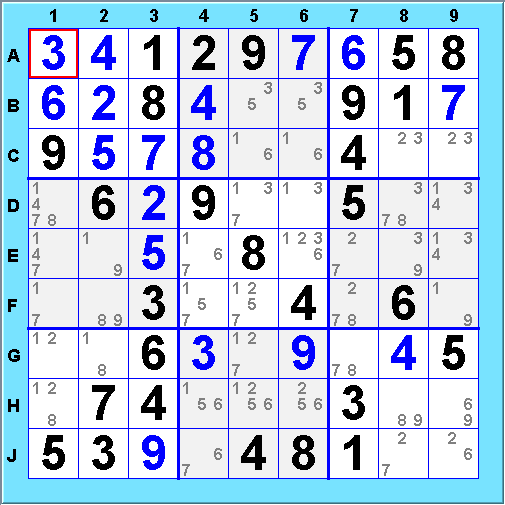
The hidden triple is in Box 6: values 2, 7 and 8 must fill D8, E7 and F7, which eliminates 3 as a possibility for D8.
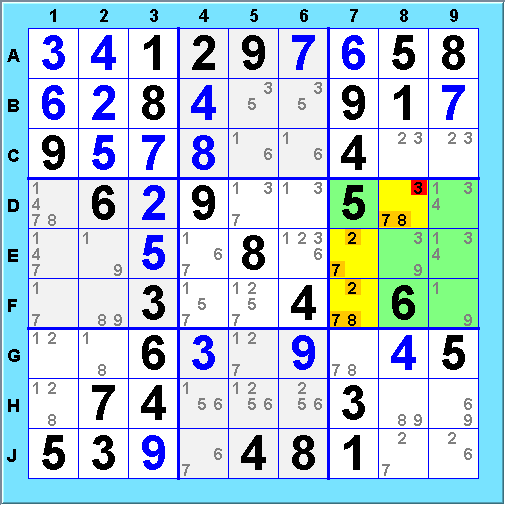
These two strategies, also called "Locked Sets", are very effective at eliminating possibilities and applicable in a great many situations.
In the hidden pair example above, there were 6 open cells in Column 3, of which B3 and E3 formed a hidden pair. If you examine the possibilities in the remaining 4 cells - C3, F3, G3, and J3 - you will see they form a naked quad. A little thought shows that useful Naked and Hidden sets are complementary situations.
Suppose we identify a Naked Set in some group. Call that set of cells S and their set of possibilities P(S). Let set C be the remaining open cells of the group, and P(C) their set of possibilities. If P(S) and P(C) are have no values in common then C is naked also and no possibilities can be eliminated. A naked set is useful when P(S) and P(C) share some values, because those can be eliminated from C. Lets focus on that case.
If the puzzle is solvable, the set of unshared values P(C)-P(S) must have exactly as many values as C has cells. That means C and P(C)-P(S) constitute a Hidden Set: C is a set of cells whose possibilities P(C) include values P(C)-P(S) which only occur in C and therefore must be assigned to C, plus some extra values which must be eliminated since there's no room for them.
This argument also shows that the Naked Set and its complement Hidden Set eliminate exactly the same set of possibilities. A similar argument shows that when you find a Hidden Set, the remaining open cells of its group must constitute a Naked Set. Look back at the other Naked and Hidden set examples to find to the complement sets.
In solving a puzzle we prefer to use the simplest strategies first, and for a given strategy, the simplest or smallest instance. Since Naked and Hidden sets are complementary, we really need only search for one type. If we find a naked set of size 3 is a group with 5 open cells, we can report the complementary hidden pair of size 2. A bit of care is required, as a complement set is not necessarily minimal, even if the original set is. Consider a group with 6 open cells, the first two having possibilities (1,2), the next 2 having (1,2,3,4), and the last two (1,2,3,4,5,6). The first 2 cells form a Naked Set. From that we can infer that there is a Hidden set (3,4,5,6) on the other 4 cells. However, this set isn't minimal - there is a smaller hidden set on (5,6) in the last two cells.
The Group Intersection strategy looks at the relationships between the possibilities in pairs of groups. When two groups share cells, the possible location of values in one can be constrained by the possibilities in the other. Take any two groups which share some set of cells. If it happens that for Group 1, the only possible cells for value v are within the shared cells, then we can eliminate v as a possibility from all the unshared cells of Group 2. Why? Placing v in the non-shared cells of Group 2 would eliminate it from the shared cells, leaving Group 1 with no cell left for v! Try to find a situation of this type in the following puzzle. Hint - look at the value 5:

Look at the distribution of 5's - Row B (blue)has all its 5's in cells shared with Box 2 (green). One of these shared cells must contain a 5, eliminating 5 from A5. This elimination can also be found by another intersection: Box 3 has all its 5's in cells shared with Row A, also eliminating 5@A5.
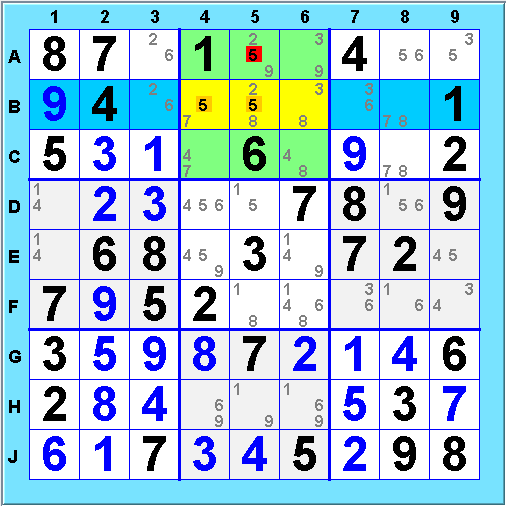
This strategy is also known as "Pointing Pairs" and "Box-Line Reduction".
The rules of sudoku give us lots of exclusion links - for each possible choice a@A, there is an exclusion relationship from a@A to each other value in cell A and to value a in every cell sharing a group with cell A. Call these weak links. Forcing relations arise when there remain only 2 choices that satisfy some requirement, because then excluding either choice forces the other. Call these strong links, as they provide forcing in addition to exclusion. Strong links allow us to glue together weak links into chains of inference. An inference chain is any sequence of links where at least every other link is strong.
Whenever such a inference chain forms a loop, or cycle, it can give us additional eliminations. When the length of a cycle is even, it allows us to promote the weak links to strong and eliminate competing alternatives outside the cycle. When the length of the cycle is odd, the cycle cannot be satisfied meaning that some choice within the cycle can be eliminated. Very complex chains can be formed, some of which can be devilishly hard to find. We will start with two restricted types of inference chains that are common and relatively easy to find: X-cycles, which are chains of choices related to one single value, and XY-chains, which are chains linking cells with only 2 possibilities ("bivalue cells"). General inference chains will be covered under the Extreme strategies.
An X-Cycle is a cycle of choices all involving the same value. It is helpful in visualizing these to make a diagram of the links such as shown here. We have highlighted the possible choices and links for the value 4 by clicking on the "4" in the column headings and enabling the Link display option. Weak links are shown in green and strong links in red. What cycles can we find here?
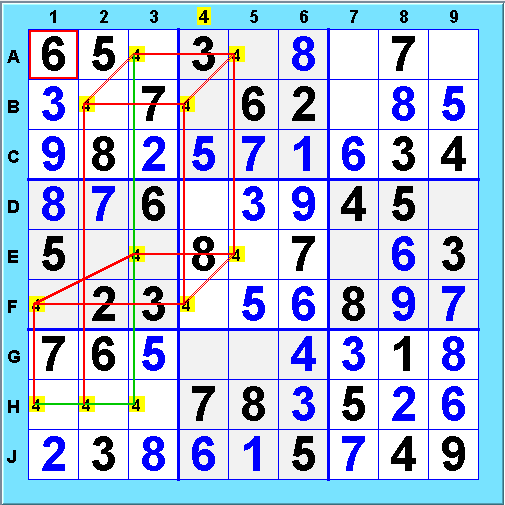
One X-cycle goes through A3, E3, E5, and A5, as shown below. The cycle is written
where "-" and "=" stand for weak and strong links respectively. One of the "weak" link positions in the alternation is occupied by strong link, indicated by "--" and shown in blue when the cycle is displayed:
What can we infer from this cycle? Consider the 4@A3-4@E3 weak link. This link means that if 4@A3 is chosen, 4@E3 is eliminated. What if 4@A3 is eliminated? Following the 4@A3=4@A5 link, we find that if 4@A3 is eliminated, 4@A5 is forced, which eliminates 4@E5, which forces 4@E3. Because of the cycle, one of 4@A3 and 4@E3 must be selected, and therefore all other choices weak-linked to both 4@A3 and 4@E3 can be removed. In this case that is 4@H3. In effect, a regular X-cycle promotes each of its weak links to strong. This is a powerful strategy because it can eliminate many possibilities in a single step. Much longer X-cycles are possible. Use value highlighting plus links display to focus on X links.
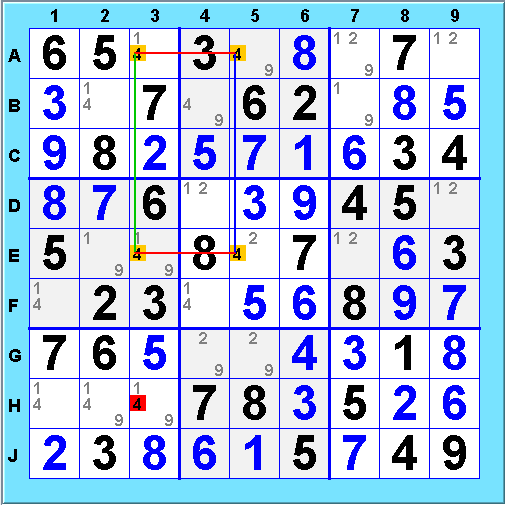
Odd-length X-Cycles turn out to be useful also, but the logic is different. Consider an odd-length X-cycle that is alternating except for one choice point where there are two weak links in a row. In the example below, that would be 4@C6 in the cycle
Consider one of the strong links near 4@C6, say 4@D4=4@F6. The strong link tells us that one of these choices must be selected. If 4@F6 is chosen, the weak link 4@F6-4@C6 means that 4@C6 is eliminated. What if 4@D6 is chosen? The chain shows that 4@C6 is eliminated in that case also. 4@C6 is eliminated no matter which of 4@D4 and 4@F6 is chosen, so this "weak" X-Cycle eliminates 4@C6 unconditionally. Weak X-cycles are more common than regular ones and therefore a very useful technique.
What about an odd-length X-cycle that is alternating except for one choice point where there are two strong links in a row? Here is an X-Cycle of length 5
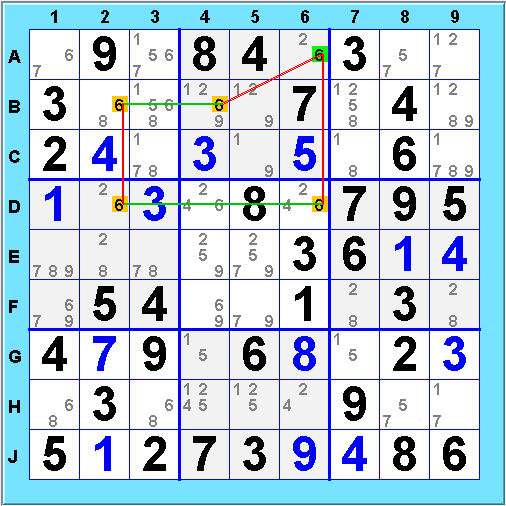
In this case the distinguished choice point is forced instead of eliminated. Let's see how this works. If 6@A6 were eliminated, that would force 6@B4, which forces 6@D2, which forces 6@A6 - a contradiction! If 6@A6 is selected, the two adjacent choices are eliminated but since the subsequent links are weak, further inferences stop and contradiction is avoided. The X-Cycle forces A6 to be 6 (and in this case, solves the puzzle).
One can save some effort by seeing that strong x-cycles are just a special case of weak x-cycles. In the example above, if we treated the 6@A6=6@B4 link as a weak link rather than a strong one, we would have a weak x-cycle, eliminating B4. Since 6@A6=6@B4 is a strong link, A6 would be forced immediately. So we don't really need to search separately for strong x-cycles - as long as we find the weak x-cycles, in any case where its actually a strong x-cycle the forced choice will be evident immediately after.
In X-Cycles we focused on a single value to reduce the number of links we needed to consider and make the search more manageable. XY-Cycles remove that restriction by focusing on bivalue cells - cells with just 2 possibilities. Often as we continue to eliminate possibilities there come to be a number of bivalue cells. Since each such cell provides a strong link between its two possibilities, they easily form inference chains anywhere two such cells with the same possibility share a group. Such an inference chain is called a XY Chain. XY chains come in the same range of configuration we saw with X-Cycles: regular, weak, and strong. Here is a length-10 regular XY Chain
which removes 1 from D3:

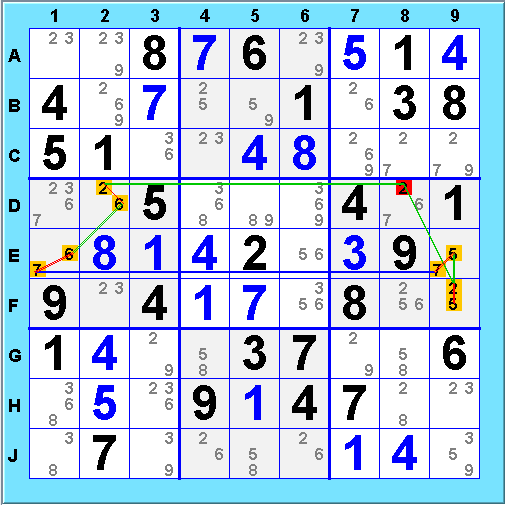
Here is an odd-length weak XY Chain. It eliminates 2@D8 because it is at the junction of two weak links.
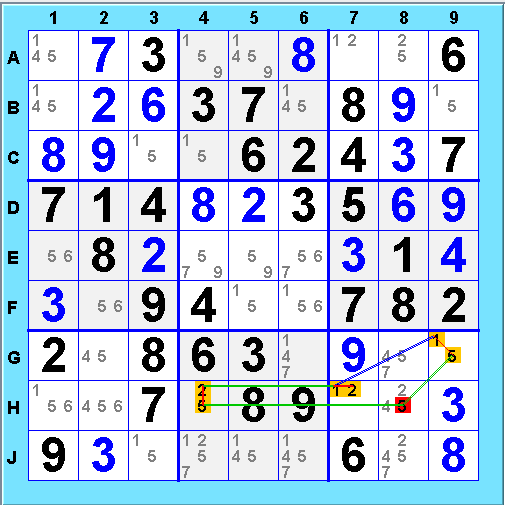
The shortest odd XY Chain in a regular Sudoku requires 3 bivalue cells (7 links). This configuration is called a Y Wing. Here is a Y Wing that eliminates 5@H8:
Highlighting plus link display was an effective aid for finding X-cycles, but for hunting multiple-value chains like the XY such a simple approach -- showing all the links -- typically yields an unreadable display. The Solver provides some specialized views to reduce this clutter. Selecting View>Select View>XY Chains highlights the key strong links within the bivalue cells in red, plus only those additional links that chain those links together. The additional links are colored green for weak and blue for strong, so the bivalue links are clear. Here is the XY view for the position containing the length-10 regular XY chain example above. The chain possibilities stand out and the example chain should be relatively easy to find.
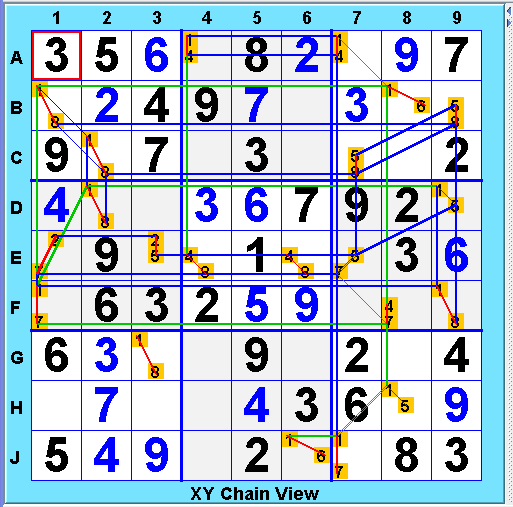
Exercise for the reader: there is a length-15 weak XY chain in this position also - can you find it?
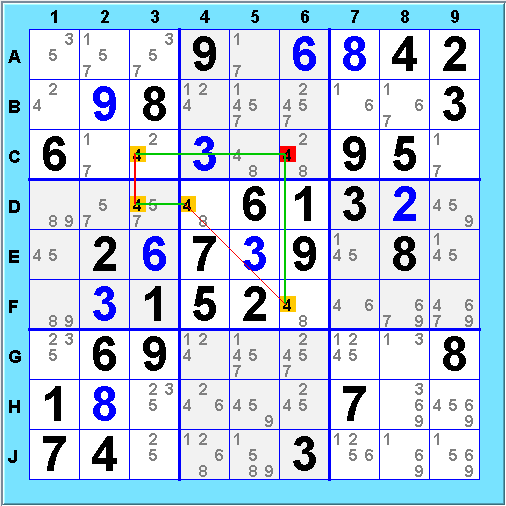
An X-Cycle chain has to be at least 4 links long to be useful, so to make one we need at least 2 strong links that are in a position to be chained. Often one encounters situations lacking strong links or with strong links not well positioned for chaining. Grouping enables us to conjure strong links out of weak ones. Here is an example - there are lots of weak links on value 1, but there are no useful X-Cycles available:

The trick here is that the exclusion relationships we have represented by links can apply to sets of choices as well as individual ones. Wherever a box intersects a row or column and a value appears in more than one cell of the intersection, there is an opportunity to generate a strong link to the set of cells containing that value. The intersection of Box 1 and Column 1 is an example. Taking 1@A1 and 1@C1 individually, we get only weak links. If we group them, we generate a strong link 1@A1C1=1@J1. This link means "We must assign value 1 to either J1 or one of (A1, C1)". We also need to include links from Box 1. Since there are multiple cells where 1 can go in Box 1 besides A1 and C1, we get weak links from 1@A1C1 to each of A2, A3, and C3. This is enough to give us a useful cycle
which eliminates 1@A2;
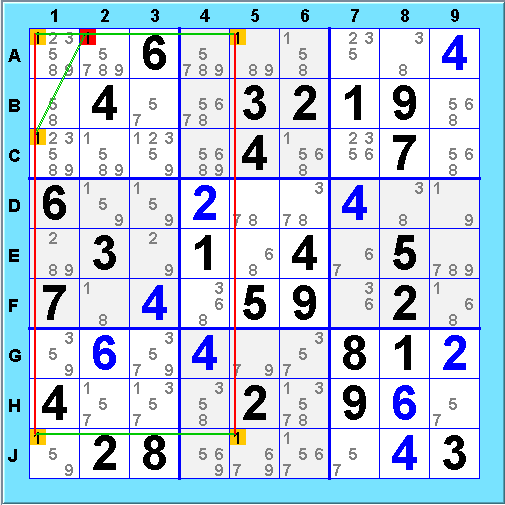
Grouped links are represented in the diagram by individual links to all members of the group. The logic is exactly like that for a regular x-cycle: if 1@A2 is selected, that eliminates 1@A1 and 1@B1, and when both of those are eliminated, 1@J1 is forced, eliminating 1@J5, forcing 1@A5 - a contradiction. So 1@A2 can be eliminated.
Chains can be built with multiple grouped nodes. Here's a multi-group cycle
that removes 6@B6:
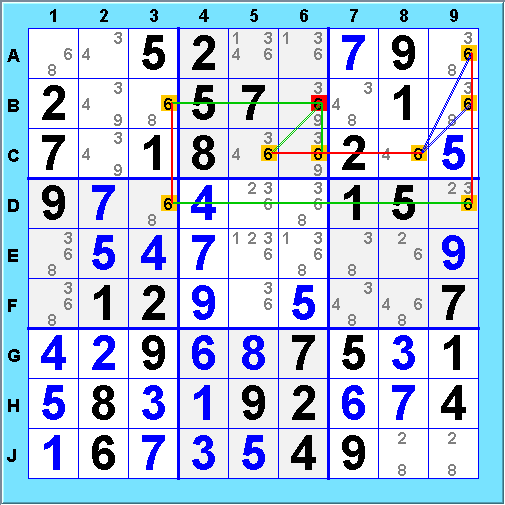
When forming chains, group-to-group links are also important, as in this example. The weak cycle
eliminates the grouped node 2@G2H2J2:

Another way of eliminating candidates is based on the presumed uniqueness of the solution. In the following puzzle, consider cells D1, D5, E1, and E5. Suppose we assigned 3 to D1, which would force 6@D5, 3@E5, and 6@E1, and we were able to find a solution from there. In that solution we could swap 3 and 6's among those 4 cells and all the containing groups - Columns 1 and 5, Rows D and E, and Boxes 4 and 5 - would still contain exactly one 3 and one 6. That means the puzzle would have 2 solutions (at least). Assuming the puzzle is well-formed with a unique solution, 3@D1 cannot be part of the solution. We can eliminate 6@D1 likewise, leaving only 8 as a possibility for D1. This strategy typically involves a rectangle of 4 cells and so is called the Unique Rectangle.

The general logic is this: If a Sudoku solution contains a rectangle of 4 cells filled with exactly 2 values, and the cells belong to exactly two boxes, then it contains a "non-unique rectangle" in which the values in the cells can be swapped without violating any of the rules. If the puzzle solution is unique, then any choice which forces such a rectangle to occur cannot be part of that solution and can be eliminated. (More complex configurations with swappable values exist, but we will focus on rectangles only here.)
There are several ways to identify such cases. The simplest case, type 1, occurs when 3 cells of a rectangle contain only a pair of possibilities ab and the fourth cell contains the same two possibilities plus any number of additional values. In that case, filling the fourth cell with either a or b would create a non-unique rectangle, so possibilities a and b can be eliminated from the fourth cell. The example above is a type-1 unique rectangle.
A type 2 unique rectangle occurs when 2 cells of a rectangle contain only a pair of possibilities a and b and the other two cells C and D contain a and b plus one additional possibility c. In that case, one of C and D must contain c, so c can be eliminated from any cells sharing a group with C and D. This puzzle contains a type-2 unique rectangle at A3, C3, A5 and C5 on values 5 and 7. Value 6 must be assigned to one of A5 and C5 or a non-unique rectangle will be created. This eliminates 6 from A6 and J5.

A type 4 unique rectangle is a situation where 2 cells of a rectangle contain only a pair of possibilities a and b, the other cells C and D contain a and b plus any number of additional values, and there is a strong link between a@C and a@D. In that case, selecting b@C would force a@D, creating a non-unique rectangle; ditto b@D. So b can be eliminated from C and D. The next example is a type-4 unique rectangle at D5, H5, D6 and H6: Value 2 must go in one of D6 and H6. So we must eliminate 5 from D6 and H6.

In the type-4 case we saw how one strong linkage could create a nonunique-rectangle configuration. Generalizing, we define a Hidden Rectangle as a rectangle of four cells containing a common pair of possibilities a and b, with strong links on a and/or b between cells such that selecting a or b at one of the cells forces a non-unique rectangle. An example will help make this more concrete. Here, three cells of a rectangle have possibilities beyond the shared pair, but the strong links 6@G3=6@E3 and 6@E1=6@G1 cause 7@G3 to force a non-unique rectangle.
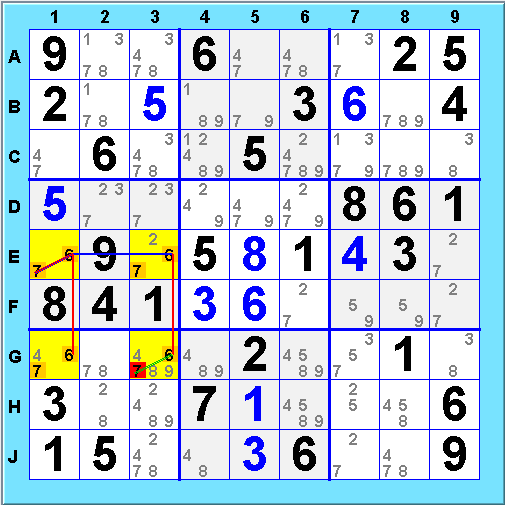
In discussing X-Cycles and XY Chains we focused on restricted forms of chains that are easier to find. This is not always sufficient. In many cases a useful chain can only be formed by considering inference chains composed of alternating strong and weak links with no other restriction (AICs). Such chains typically look like sets of X and XY chains "glued" together. Here is an example of a weak AIC:
Here a weak cycle
composed of subchains on 1,2, and 9 eliminates 9@B1.
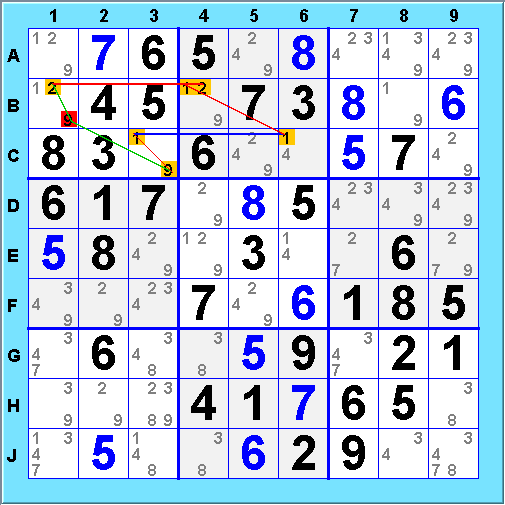
Here is an example of a strong AIC:
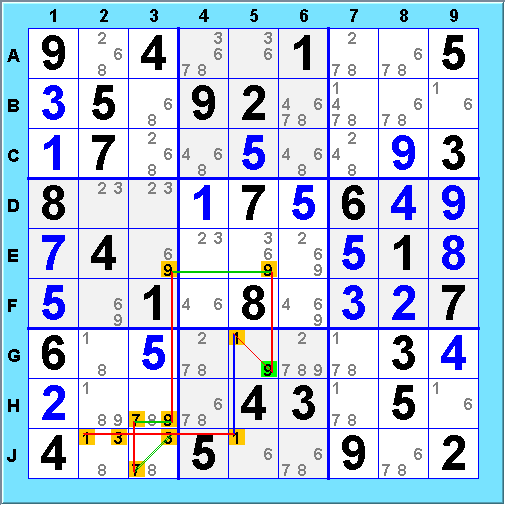
The strong cycle
forces 9@G5.
View>Select View>AIC provides an aid in locating AICs by highlighting all strong links in red, plus only those weak links that chain strong links together.
What about other Sudoku sizes than the standard 9x9? If one wants to keep the box regions square, the best option is 16x16. Such puzzles are published and manageable, though a bit large. If we allow rectangular regions, we have a much larger range of options - the Library contains puzzles in a range of difficuclties in size 6x6, 8x8, 10x10, 12x12, and 15x15. (We omitted 14x14 as the 2x7 regions seem ugly.) All the strategies we have discussed work exactly the same with rectangular regions as with square ones. The prime sizes 7x7, 11x11, and 13x13 can be used but would necessarily have jigsaw regions - more about the consequences of that in the next section.
Jigsaw Sudoku are sudoku with non-rectangular regions. All the strategies described above still apply, with the difference that in place of groups created by rectangular boxes we have groups created by non-rectangular regions.
With more irregular regions there are more intersections to work with. Here is a group-intersection example: Region 4 has all its 1's in cells shared with Row D, which removes 1 from D5, 1 from D6.
Due to the irregular shapes of the regions, our strategies can sometimes apply in new ways. Non-rectangular regions can intersect with *both* the row and column groups of external cells, which means that the minimum length of X-cycles can be shorter than in regular sudoku. We call these micro-cycles and chains. In the example below, a micro X-Cycle eliminates 7@C5 because it is at the junction of two weak links:

This example shows that in a jigsaw sudoku loops of links can be created by the intersection of 3 groups, here Region 2, Row C, and Column 4. Such a loop requires at least 4 groups in a regular Sudoku.
Grouped X-cycles also occur in short versions. Here, cycle
eliminates 4@F1:
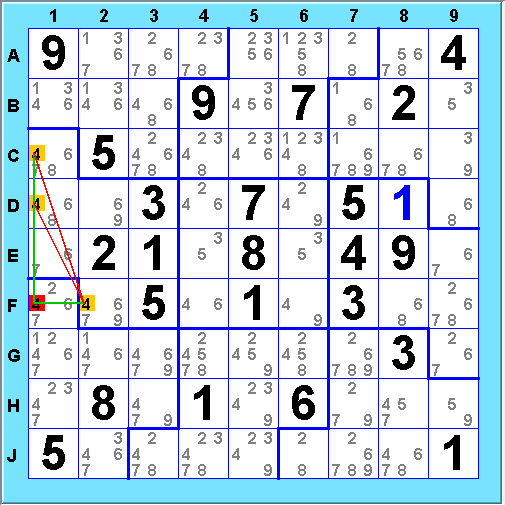
Y Wing formations can be formed using just 2 bivalue cells in jigsaw sudoku, as opposed to a minimum of 3 in regular sudoku. Here, a micro Y-Wing eliminates 4@E4:
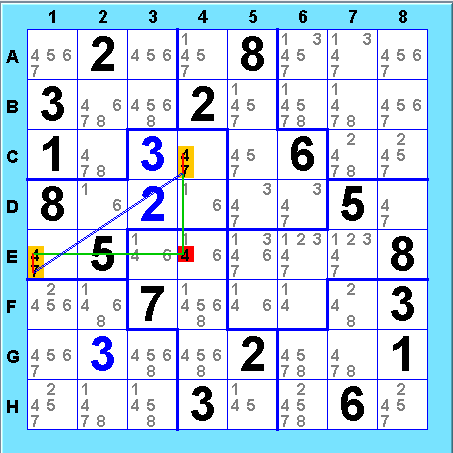
Here is an X-cycle containing multiple grouped nodes:
This weak cycle eliminates 5@D2D3, removing two possibilities at once.

Explanations and illustrations of advanced Sudoku solving strategies can be found at
Puzzles
| Home | Run Solver | User Guide | Programming |
|---|